Les angles

1. Définition

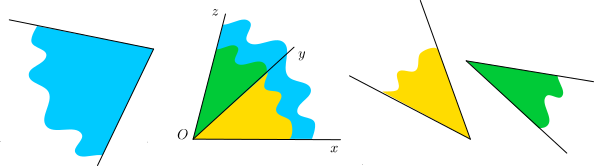
Deux demi-droites ayant la même origine partagent le plan en deux surfaces.

La surface orange est un angle saillant, la surface bleue est un angle rentrant. Le point O est leur sommet, les demi-droites et sont leurs côtés. Les deux demi-droites réunies forment la frontière entre les deux angles.

Le plus souvent on notera l’angle saillant.

Si les demi-droites sont dans le prolongement l’une de l’autre, le plan est partagé en demi-plans, on parle alors d’angles plats.

2. Comparaison

Dans la figure suivante, l’angle est contenu dans l’angle .

L’angle est alors plus petit que l’angle .

Plus généralement, si est égal à un angle situé à l’intérieur de , alors est plus petit que .

3. Angles adjacents et somme

Une droite passant par le point O partage l’angle en deux angles.

Les angles et sont adjacents. Deux angles adjacents ont le sommet commun, un côté commun et sont situés de part et d’autre de ce côté commun.

Les angles adjacents et forment l’angle .

On dit de tout angle égal à qu’il est la somme d’un angle égal à et d’un angle égale à .

4. Angles opposés par le sommet

Deux droites et sécantes en un point déterminent quatre angles.

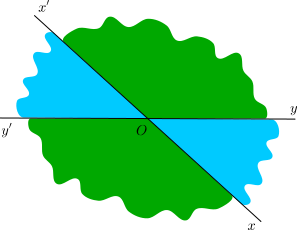
• les angles et sont dits opposés par le sommet,
• les angles et sont opposés par le sommet.

 

Théorème. Deux angles opposés par le sommets sont égaux.

5. Angles adjacents complémentaires

Les angles et ont le côté commun et forment un angle plat, on dit alors qu’ils sont adjacents supplémentaires.

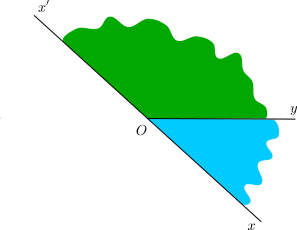
On dit que est un supplément de l’angle et que est un supplément de .

Le plus petit des deux angles est dit aigu, le plus grand est dit obtus.

Si les deux angles et sont égaux, on parle d’angles droits.

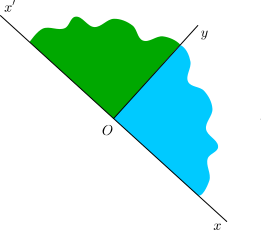
Théorème. Tous les angles droits sont égaux.

6. Angles alternes-internes

La droite coupe la droite en A et la droite en B.

• Les angles rouges et sont dits alternes-internes (entre eux)
• les angles oranges et sont alternes-internes.

Théorème. Si une droite coupe deux droites parallèles alors elle forme des angles alternes-internes égaux.

Réciproquement, si une droite coupe deux droites et forme des angles alternes-internes égaux alors les deux droites sont parallèles.

7. Angles correspondants

La droite coupe la droite en A et la droite en B.

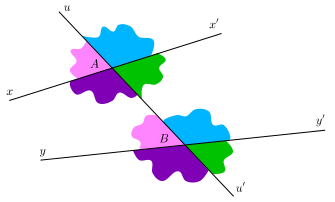
• Les angles roses et sont dits correspondants (entre eux),
• les anges violets et sont correspondants,
• les angles verts et sont correspondants,
• les angles bleus et sont correspondants.

Théorème. Si une droite coupe deux droites parallèles alors elle forme des angles correspondants égaux.

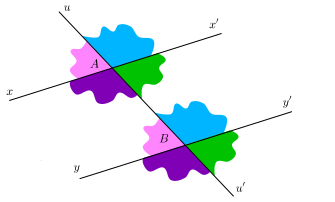
Réciproquement, si une droite coupe deux droites et forme des angles correspondants égaux alors les deux droites sont parallèles.